Often we use inverse as a synonym of opposite in real life. In maths also the inverse of a matrix represents the reciprocal of the matrix. In this article, let us know more about the inverse of matrices. As you know matrix is a rectangular array of numbers arranged in rows and columns.
Ex: A =
| 1 | 2 | 3 |
| 2 | 1 | 3 |
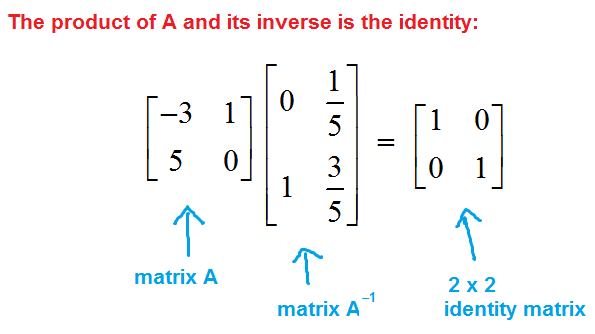
If A and B are square matrices of order m × m, such that AB = BA = Im , then, A is said to be an invertible matrix and B is called the inverse matrix of A. The inverse of A is written as A-1. The inverse of a matrix is that matrix which when multiplied with the given matrix forms the multiplicative identity. For a matrix B, its inverse is B-1, and B B-1 = I. The general formula to find the inverse of a matrix is equal to the ratio of adjoint of a matrix to its determinant.
A =
| p | q | |
| r | s |
A -1 = 1AadjA
Where A = 1ps – qr and
Adj A =
| s | -q | |
| -r | p |
Terms Used in Inverse of a Matrix
Minor of a matrix: It is defined as the determinant of a square matrix. In a matrix if you have to find the minor of an element then eliminate the row and column containing that element. The matrix of remaining elements is formed, this represents the minor of a matrix.
Cofactor: cofactors are the number obtained when you eliminate the row and column of a particular element in a matrix, which is just a grid in the form of a square or a rectangle.
Let P be any matrix of order m x m and Mij be the (m – 1) x (m – 1) matrix obtained by deleting the ith row and jth column. Then, det(Mij) is called the minor of aij.
We can find the cofactor Cij of aij using the formula: Cij = (−1)i+j det(Mij)
Determinant: The determinant of a matrix is a value that is defined only for square matrices. The determinant of the matrix is equal to the summation of the product of the elements and its cofactors of a particular row or column of the matrix.
Singular Matrix: A matrix with a determinant value as zero is referred to as a singular matrix. For a singular matrix P, |P| = 0. There is no inverse for a singular matrix.
Non-Singular Matrix: in a non-singular matrix the determinant value is not equal to zero. For a non-singular matrix |B| ≠ 0. A non-singular matrix is also called an invertible matrix.
Adjoint of Matrix: Let P = [aij] be a square matrix of order n . The adjoint of a matrix P is the transpose of the cofactor matrix of P . It is denoted by adj P.
Methods Involved in Finding the Inverse of a Matrix:
One can find the inverse of a matrix using the following methods.
1. Elementary Row or column transformations.
These are the operations performed on rows and columns of the matrices to transform it into a form that makes the calculations easier. The concept of ‘Elementary row and column transformations’ are used in the gaussian method of solving linear equations, finding the inverse of the matrices, etc. the order of the two matrices must be the same to perform elementary transformations between any two matrices.
2. Using inverse matrix formula:
As we discussed above the general formula to find the inverse of a matrix is used.
A -1 = 1AadjA
Where A = 1ps – qr and
Adj A =
| s | -q | |
| -r | p |
For more detailed information regarding how to use row and column transformations and solved examples log on to the Cuemath website.