Basically, ordering is a sequence of things and it is used for many purposes. Sometimes we have to order things by comparing its weight (which one is heavier or lighter), sizes (which one is small or large) heights etc. We order the things according to our requirements. We also arrangethings by comparing its lengths, measurements and nature of commodity.
Placing the numbers in a sequence or series is called ordering numbers. Numbers can be arranged in two ways:
- Ascending Order
- Descending Order
Such arrangement of numbers in a series which begins with the least and ends with the greatest or largest number is known as ascending order whereas, in contrary, arrangement of numbers from largest to smallest in a sequence is called descending order.
For Example
2, 4 , 6 , 8 , 10 Ascending order (Smallest to greatest arrangement of numbers)
10 , 8 , 6 , 4 , 2 Descending Order (greatest to smallest arrangement of numbers)
Similarly decimals and fractions are also placed in ascending and descending order by comparing the smallest and largest values according to the requirement.
There are two methods of ordering fractions:
- Converting the fraction into decimal before ordering
- Common dominatormethod
Converting the fraction into decimal before ordering
The fraction values are converted into decimal before ordering in a sequence.
Example:
Arrange the following fraction in ascending order
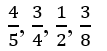
Solution:
Given fractions are 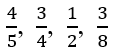
Convert all fractions into decimal
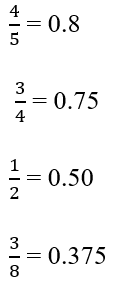
New decimal values are
0.8, 0.75, 0.50, 0.375
Compare the decimal values at tenth’s digit with each other and arrange in ascending order to get the answer
0.375, 0.50, 0.75, 0.8
The fractions can also be solved by calculating their percentages and comparing it with each other.
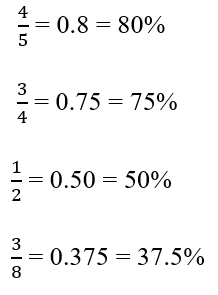
Now compare the integer values and writer in ascending order
37.5%, 50%, 75%, 80%
Common dominator method
Another method of ordering fraction is common dominator. In this method, numerators are compared by determining their equivalent fractions with the common dominator. For this purpose, common dominator is formed by using multiples of two numbers.
For Example, The common multiple of 4 & 3 is 12. There are many other multiples of 4 & 3 but 12 is the least common multiple.
Our main concern in this topic is to familiarize yourself with the numbers, decimal and fractions from least to greatest ordering arrangements which is also considered as ascending order. For this purpose following examples are given below to understand the concept of ordering. You can also find the ascending or descending arrangement of numbers, decimals, fractions and percentages by using least to greatest.
Examples of ordering numbers, decimals and fractions:
Example 1:
Arrange the order of the following number from least to greatest?
24, 63 , 42 , 55
Solution:
Given numbers are
24 , 63 , 42 , 55
Simplify
24 = 2 x 2 x 2 x 2 = 16
63 = 6 x 6 x 6 = 216
42 = 4 x 4 = 16
55= 5 x 5 x 5 x 5 x 5 = 3125
New numbers are
16 , 216 , 16 , 3125
Now arranging the numbers from least to greatest value orascending order
16 , 16 , 216 , 3125
Example 2
Arrange the fractions from least to greatest order by using common dominator method?
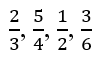
Solution:
Given is 
In common dominator method, first of all find all the dominators of the given fractions. The upper part of the fraction is called numerator and the lower part is called dominator.

We have the dominator 3, 4, 2 and 6
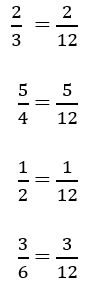
The least common multiple of the dominator 3, 4, 2 & 6 is 12. Therefore we can write that
Now all the fractions have same dominator so compare the values of numerators to arrange the values in ascending order
1 < 2 < 3 < 5
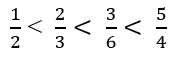
Example 3
Arrange the fractions from least to greatest order by converting it into decimal?
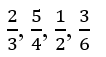
Solution:
Given fractions are
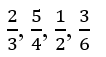
Convert each fraction into decimal

Comparing the decimal values
The value 1.25 is greater than all other values so we place this at last position in ascending order
The value 0.50 is smallest than all other values so we place this at first position in ascending order
Therefore the arrangement is as under:
0.50 , 0.50 , 0.66 , 1.25
Example 4:
Arrange the numbers in ascending and descending order?
39, 28, 47, 56
Solution:
Given numbers are
39, 28, 47, 56
Simplify the numbers
39= 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 19,683
28= 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256
47 = 4 x 4 x 4 x 4 x 4 x 4 x 4 = 16,384
56 = 5 x 5 x 5 x 5 x 5 x 5 = 15,625
New numbers are
19,683 , 256 , 16,384 , 15,625
Arrange the new numbers in ascending order. You can also use least to greatest calculator for this purpose.
256 , 15625 , 16384 , 19683
Arrange the new numbers in descending order
19683 , 16384 , 15625 , 256,
Therefore we can write the actual given numbers in ascending and descending order as
28, 56 , 47, 39 (Ascending order)
39,47 , 56 ,28(Descending order)