What is an increase outline?
A duplication outline (some of the time otherwise called an increase table or augmentation matrix) is a unimaginably supportive number related instrument.
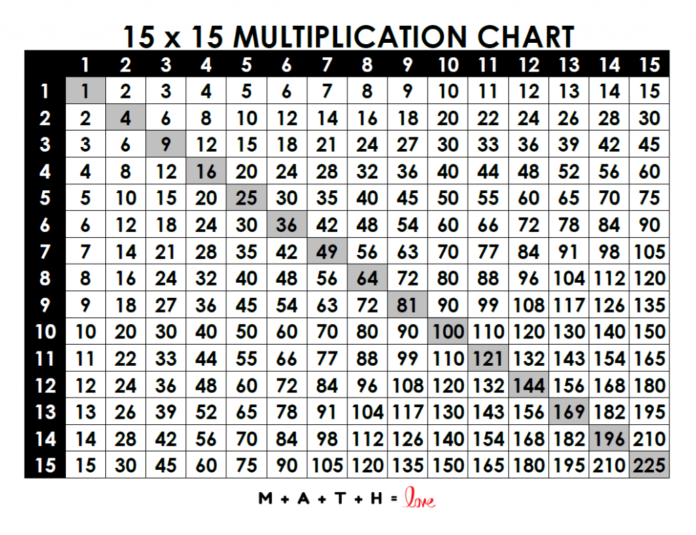
It shows times tables in network structure like so:
duplication outline for 1 to 10
The duplication outline above shows all times tables from 1 to 10.
You can find (in the yellow boxes) that the numbers 1 to 10 run on a level plane along top of the diagram and they likewise shabby the left hand side too.
You can see from the photos beneath that on a duplication graph, each times table runs both on a level plane…
augmentation lattice showing times tables evenly
…also, in an upward direction:
augmentation table appearance times tables upward
Presently while the above graph shows times tables from 1s up to 10s, some increase outlines might kickoff tables up to 12s. In principle duplication outlines can have boundless times tables (despite the fact that assuming there are such a large number of it very well might be difficult to fit them generally on one piece of paper… )
The splendid thing about an increase outline is that you can utilize it to find the result of two numbers rapidly.
This is truly useful when a youngster is learning or reconsidering their increase realities.
We should investigate.
(Psst! At the point when you’ve wrapped up perusing this post, remember to have a peruse of my other free exercises in the Free Printables Library!)
How would you utilize an increase diagram?
It’s truly simple to find the result of two numbers utilizing this graph.
The most effective way to make sense of this is to utilize a model.
Thus, suppose we need to understand what 5 x 4 is.
To see as 5 x 4, we should find the line that shows the multiple times tables and the segment that shows the multiple times table. Then we search for the crate where the they cross-over:
multiplicaiton table showig that 20 is the result of 4 and 6
As you can see here, the 5 line and 4 section cross-over here at the number 20.
So the outline lets us know that 5 x 4 = 20 (which is right – whoopee!).
Another model?
We should accept another model, say 9 x 6.
First find the line with every one of the products of 9. Next track down the segment with the products of 6.
graph showing 9 x 6
Follow the two lines along until they meet. The container where they cross-over will let you know the result of 9 and 6. Furthermore, that is 54. Check!
Does the request matter?
Presently the extraordinary thing about augmentation is that the request for the two number you are increasing doesn’t make any difference.
For instance 9 x 6 is equivalent to 6 x 9. Or then again 2 x 8 is equivalent to 8 x 2.
Furthermore, this is likewise valid for the duplication graph.
How about we glance back at our 9 x 6 model.
You can see by taking a gander at the diagram beneath that it doesn’t make any difference whether you take the line of 6s and the segment of 9s or the column of 9s and the section of 6s. You actually find the solution 54:
duplication table appearance 6 x 9 and 9 x 6
Sharp, eh?
As a matter of fact, assuming you look carefully, you’ll see that the graph can be isolated into equal parts with an inclining line from the increase sign down to the base corner with the number 100.
duplication matrix showing square numbers
The numbers in the base piece of the diagram are reflected in the top part. Furthermore, whether you utilize the top part to find the result of two numbers or the base piece of the graph, the response will be something similar.
Related: ‘Be an increase star!’ – Guard bunch of times tables worksheets for serious numerical realities practice!
For what reason is an increase outline supportive?
An increase diagram is truly helpful for various reasons:
- It’s a convenient reference device
A duplication outline is so important on the grounds that it shows every one of the times tables plainly in only one network. It’s a convenient reference instrument for kids who need to learn and retain their duplication realities.
A duplication lattice like this can likewise be truly useful in circumstance when a youngster needs to figure out duplication realities to rehearse an alternate number related expertise.
For instance, a kid who’s dealing with finding areas of square shapes would think that it is troublesome in the event that they didn’t have the foggiest idea about their times tables (you need to duplicate the width by the length to track down the area). Having the option to involve a duplication matrix as a source of perspective implies that kid can in any case find success at finding the area of square shape despite the fact that they’re not yet ready to review their augmentation realities with certainty.
- It’s perfect for times table practice
A clear increase network or outline is an incredible method for rehearsing times tables. By filling in the outline, a kid is rehearsing each and every duplication truth from 1 x 1 up to 10 x 10 (or 12 x at least 12, contingent upon the graph!).
Having the option to review augmentation realities rapidly and precisely is so significant for kids while learning math. Times tables crop up in such countless areas of math. Additionally having the option to review augmentation realities effectively likewise proves to be handy in everyday life.
To rehearse times tables with a vacant increase lattice, you can download both a finished and void duplication graph printable toward the finish of this post.
Related post: Which times tables would it be advisable for you to learn first?
- Really great for spotting augmentation designs
A duplication diagram is an effective method for spotting designs, both in the actual outline and inside every individual times table.
For instance, we should see square numbers. A square number is the result of a number increased without help from anyone else. For instance 25 is a square number since it’s equivalent to 5 x 5. In the diagram, square numbers structure a straight corner to corner line across the outline like so:
Square numbers
Additionally, coordinated obviously in lines, you can recognize designs inside every individual times table. For instance, in the multiple times table you can see that the digit during the ones position is consistently a 0. Or on the other hand, while taking a gander at the multiple times table, the digit during the ones position diminishes by 1 as the products of 9 get greater.